一个对新手很友好的 CTF,一个很有趣的 CTF,也是让我烧了几天脑的 CTF..
有些题目令我印象深刻,于是决定在这里记录下自己的解题思路。
本次比赛官方也有发布完整的 write up:GitHub(应主办方邀请,有幸将本文投稿到了其中)
黑曜石浏览器 150
看到题目猜测是要修改 User-Agent 头,于是在 User-Agent 字串里添加了 HEICORE 字符,无果。
网上找找这个黑曜石浏览器到底是个什么玩意,发现主办方竟然真的建了一个黑曜石浏览器官网(备用)。
于是试图下载..
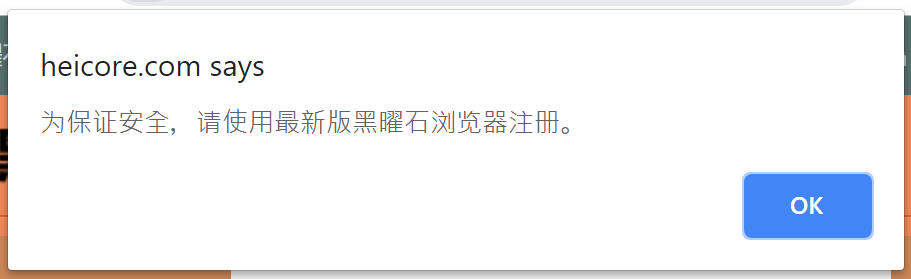
好吧那就注册一下..
(/‵Д′)/~ ╧╧
给我呈上开发者工具!然而右键似乎被网页禁止了.. 于是按下 F12..
刷新一下试试?

(/‵Д′)/~ ╧════════════╧
最后冷静下来,发现每次打开首页的时候,地址栏都会微妙的从 index.html 快速闪成 index.php,猜测是用了 history.replaceState 来进行干扰。页面实际应该是 index.html。
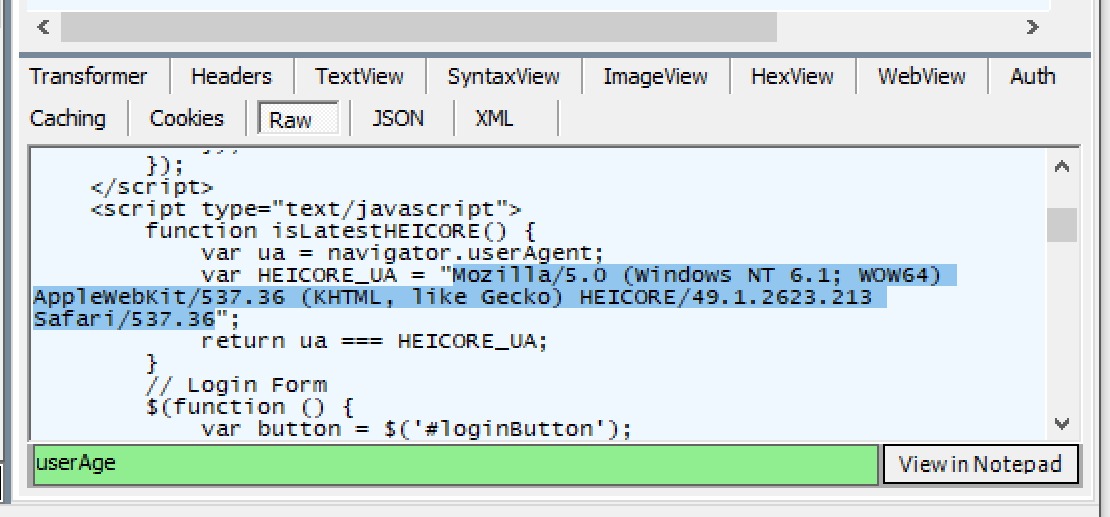
默默打开 Fiddler,配好 https 解密,清掉浏览器缓存,然后重新访问 index.html,最终找到了一堆干扰开发者工具的代码,以及最重要的, User-Agent 判断逻辑。
带上新的 User-Agent,访问最初的页面..
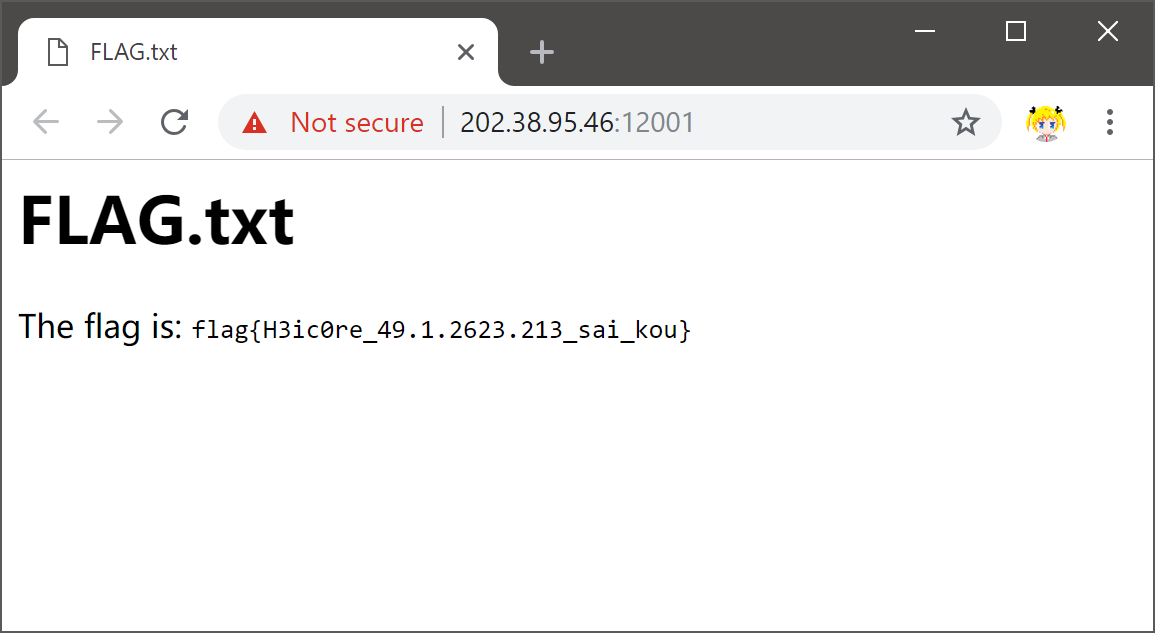
flag{H3ic0re_49.1.2623.213_sai_kou}
猫咪银行 150

总共给 10 分钟时间,每次操作都有 2 秒的限制。
一开始猜测是金融相关的题目。试试前 20 秒把 CTB 全部换成 TDSU,然后每分钟存入理财产品并取出来利滚利,总共可以存 9 轮,最终再换回 CTB。
10 CTB * 1.043^9 ≈ 14.607 CTB
FLAG 碎片售价 20 CTB,根本不够。
尝试第二种方法,注意到 CTB、RMX、TDSU 之间的兑换汇率有差异(57 * 115 < 6606),试图通过兑换来刷钱。但由于有 2 秒的时间限制,10 分钟根本刷不到 20 个 CTB。
后来又试了试理财产品能不能买入负数,果然做了判断.. 但突然想到以前一个买超大数来溢出的方法,试着对买入时间(买入份额不行)输入 MAX_INT64 (9223372036854775807),发现系统显示出现了异常。
看来这里应该就是漏洞点了。多次尝试,最终选定了 MAX_INT64 / 60 (153722867280912930) 这个数。
由于取出时间为负数,可以立即取出。获得巨款后,兑换回 CTB,最终成功购买 FLAG。
flag{Evil_Integer._Evil_Overflow.}
家里有矿 750
Z 同学为了赶上区块链的热潮,自己潜心研究工作量证明(Proof of work)算法,并且发布了三种全新的电子货币。不仅如此,他还写了一个矿池。
给专业选手的注释:此题并非 web 题,解题过程不涉及注入、XSS、敏感文件泄露、弱类型等安全问题。
提示:
1. 本题的浏览器“挖矿”只为演示性目的,几乎不占资源。我们不会以任何形式盗取或浪费大家电脑的算力。
2. 本题如果使用程序求解,对于普通配置的个人电脑,在解法正确且最优的情况下,求解程序的期望运行时间不会超过几分钟。
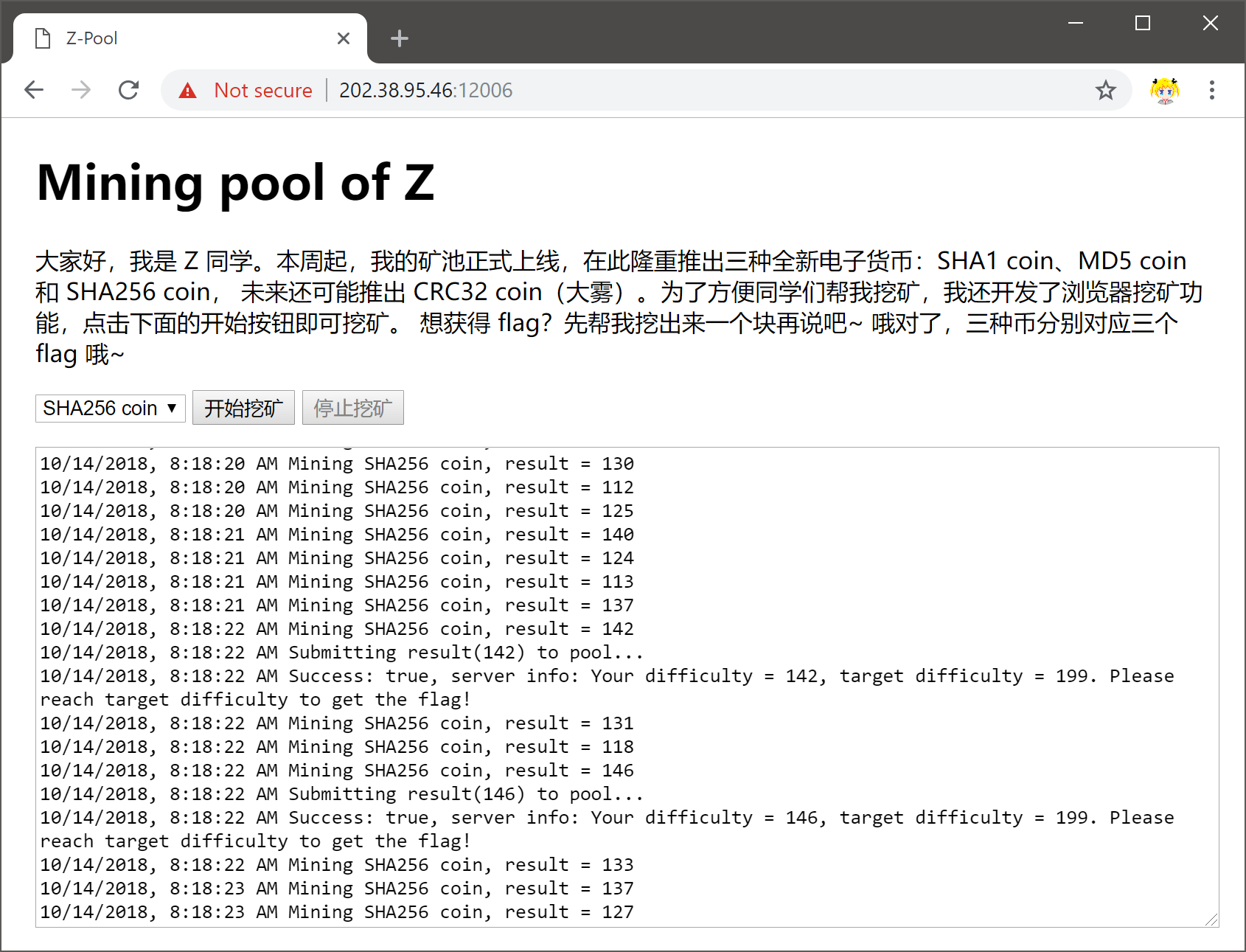
打开题目(备用)
本题包含三小题,分别是使用 SHA1、MD5、SHA256 挖矿,虽然只更换了 Hash 方法与 Suffix(后缀)长度,但三小题的解法各不相同,相当有趣。
简单分析题目,玩家可以请求服务器下发一个 Suffix,在 60 秒内,玩家需要找出两个不同的 nonce,使得:
PopCount(~(Hash(nonce1 + suffix) ^ Hash(nonce2 + suffix))) >= n // 其中 ^ 为按位异或,~ 为按位取反,PopCount 为求比特位 1 的个数, suffix 为 [a-zA-Z0-9] 内的字符 // 简单地说,就是两个 hash 中相同的比特位需不少于 n // suffix 与 n 由服务器下发 // Hash = SHA1 时,strlen(suffix) = 4,n = 140 // Hash = MD5 时,strlen(suffix) = 16,n = 102 // Hash = SHA256 时,strlen(suffix) = 1,n = 199
SHA1 150
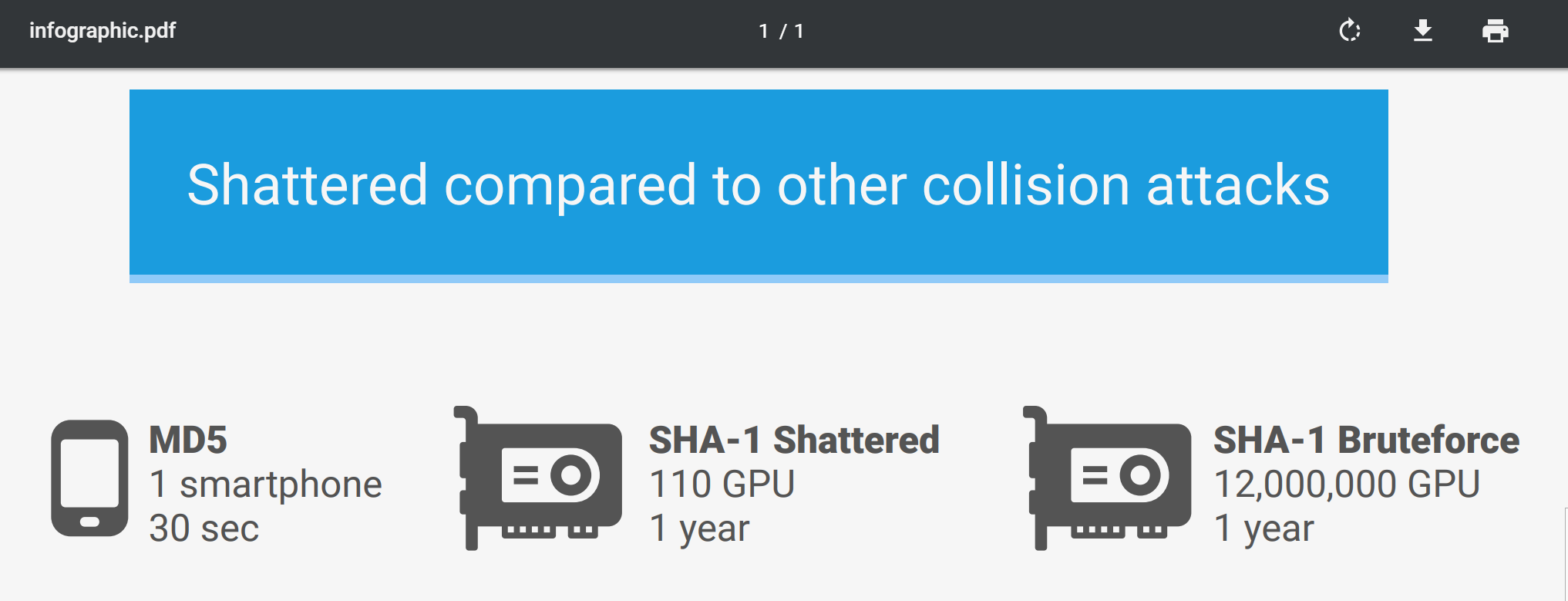
SHA1 长度 20 字节,也就是 160 bits。160 位里要撞上 140 位,相当于只能有 2.5 个字节不同,怎么想都不能硬来。
前些年谷歌正好发布过 SHA1 的碰撞,但需要 110 个 GPU 算一年,也不太现实。不管如何,先看看谷歌发布的两个碰撞样例 pdf 文件的结构。
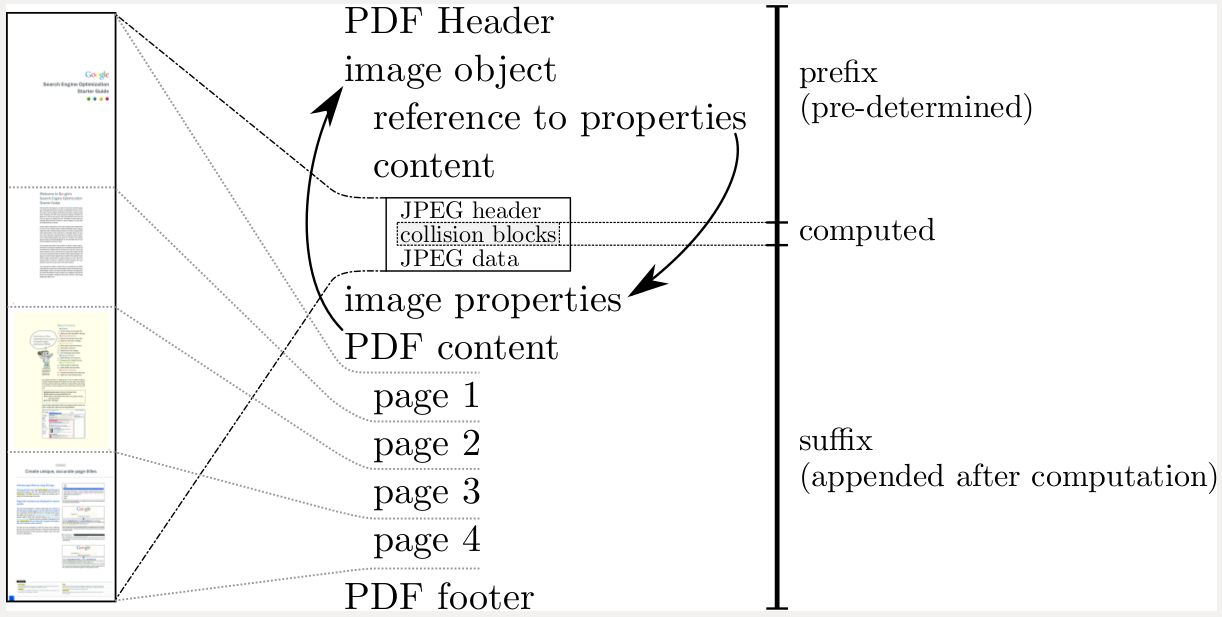
从图上看出,collision blocks 后的部分是算完碰撞后才添加的。测试后发现,同时修改两个文件的 suffix,两个文件的 sha1 依然保持一致。
这正好符合本题要求,只要用上谷歌计算好了的 prefix 及 collision blocks,使 nonce(1/2) = prefix + collision blocks(1/2),因为两块 collision blocks 是不同的,所以 nonce1 ≠ nonce2 ,但依然可以做到 sha1(nonce + suffix) == sha1(nonce2 + suffix) (PopCount = 160 >= 140)。
从网上找到 prefix 与 collision blocks,组成两个 nonce 如下:
nonce1: 25 50 44 46 2D 31 2E 33 0A 25 E2 E3 CF D3 0A 0A 0A 31 20 30 20 6F 62 6A 0A 3C 3C 2F 57 69 64 74 68 20 32 20 30 20 52 2F 48 65 69 67 68 74 20 33 20 30 20 52 2F 54 79 70 65 20 34 20 30 20 52 2F 53 75 62 74 79 70 65 20 35 20 30 20 52 2F 46 69 6C 74 65 72 20 36 20 30 20 52 2F 43 6F 6C 6F 72 53 70 61 63 65 20 37 20 30 20 52 2F 4C 65 6E 67 74 68 20 38 20 30 20 52 2F 42 69 74 73 50 65 72 43 6F 6D 70 6F 6E 65 6E 74 20 38 3E 3E 0A 73 74 72 65 61 6D 0A FF D8 FF FE 00 24 53 48 41 2D 31 20 69 73 20 64 65 61 64 21 21 21 21 21 85 2F EC 09 23 39 75 9C 39 B1 A1 C6 3C 4C 97 E1 FF FE 01 7F 46 DC 93 A6 B6 7E 01 3B 02 9A AA 1D B2 56 0B 45 CA 67 D6 88 C7 F8 4B 8C 4C 79 1F E0 2B 3D F6 14 F8 6D B1 69 09 01 C5 6B 45 C1 53 0A FE DF B7 60 38 E9 72 72 2F E7 AD 72 8F 0E 49 04 E0 46 C2 30 57 0F E9 D4 13 98 AB E1 2E F5 BC 94 2B E3 35 42 A4 80 2D 98 B5 D7 0F 2A 33 2E C3 7F AC 35 14 E7 4D DC 0F 2C C1 A8 74 CD 0C 78 30 5A 21 56 64 61 30 97 89 60 6B D0 BF 3F 98 CD A8 04 46 29 A1 nonce2: 25 50 44 46 2D 31 2E 33 0A 25 E2 E3 CF D3 0A 0A 0A 31 20 30 20 6F 62 6A 0A 3C 3C 2F 57 69 64 74 68 20 32 20 30 20 52 2F 48 65 69 67 68 74 20 33 20 30 20 52 2F 54 79 70 65 20 34 20 30 20 52 2F 53 75 62 74 79 70 65 20 35 20 30 20 52 2F 46 69 6C 74 65 72 20 36 20 30 20 52 2F 43 6F 6C 6F 72 53 70 61 63 65 20 37 20 30 20 52 2F 4C 65 6E 67 74 68 20 38 20 30 20 52 2F 42 69 74 73 50 65 72 43 6F 6D 70 6F 6E 65 6E 74 20 38 3E 3E 0A 73 74 72 65 61 6D 0A FF D8 FF FE 00 24 53 48 41 2D 31 20 69 73 20 64 65 61 64 21 21 21 21 21 85 2F EC 09 23 39 75 9C 39 B1 A1 C6 3C 4C 97 E1 FF FE 01 73 46 DC 91 66 B6 7E 11 8F 02 9A B6 21 B2 56 0F F9 CA 67 CC A8 C7 F8 5B A8 4C 79 03 0C 2B 3D E2 18 F8 6D B3 A9 09 01 D5 DF 45 C1 4F 26 FE DF B3 DC 38 E9 6A C2 2F E7 BD 72 8F 0E 45 BC E0 46 D2 3C 57 0F EB 14 13 98 BB 55 2E F5 A0 A8 2B E3 31 FE A4 80 37 B8 B5 D7 1F 0E 33 2E DF 93 AC 35 00 EB 4D DC 0D EC C1 A8 64 79 0C 78 2C 76 21 56 60 DD 30 97 91 D0 6B D0 AF 3F 98 CD A4 BC 46 29 B1
提交:
flag{sha1_21d0e7b1be5a3cae}
MD5 250
MD5 长度 16 字节,也就是 128 个比特位。128 个比特位能撞上 102 个吗?随意写了个简单的 Python 程序测试一下,发现每分钟就能撞出几个 PopCount = 97+ 的 nonce 对,再拼一把就上 102 了!
拼一把是什么操作?就是去开高 CPU 主频的 VPS 一直一直跑.. = =##
import hashlib, os, gmpy2, sys, requests, base64
def calcSet(hash1, hash2):
h2 = hash1 ^ hash2
return gmpy2.popcount(h2)
def findH(hashTail):
tail = hashTail.encode('ascii')
db = []
for i in range(18000):
hl = hashlib.md5()
d = os.urandom(10)
hl.update(d + tail)
db.append({ 'data': d, 'md5': int.from_bytes(hl.digest(), sys.byteorder) })
l = len(db)
for i in range(l):
for j in range(i + 1, l):
sets = 128 - calcSet(db[i]['md5'], db[j]['md5'])
if (sets > 95):
print(sets)
if (sets >= 102):
return { 'data1': db[i]['data'], 'data2': db[j]['data'] }
return False
while True:
req = requests.post('http://202.38.95.46:12006/getjob')
suffix = req.json()['suffix']
print(req.json())
result = findH(suffix)
if result:
req2 = requests.post('http://202.38.95.46:12006/submitjob', { \
'nonce1': base64.b64encode(result['data1']), \
'nonce2': base64.b64encode(result['data2']), \
'coin': 0
}, cookies = req.cookies)
print(req2.text)
if (req2.text.find('flag{') >= 0):
exit()
去阿里云开了台 Intel Xeon Gold 6149 3.1 GHz 的机器,跑了大概 24 小时,花了 ¥24,终于算出了碰撞..
什么?你说题目里写个人电脑只要几分钟就能碰撞出来?emmm.. 主办方大概用的 C 写的,性能比 Python 好太多了,要不就是我的算法写得太烂。
没事.. 算法烂,CPU 来凑,就是稍微有点贵..
P.S. 网上的 MD5 快速碰撞算法基本都是用于固定 prefix(前缀)的,而本题需要的是固定 suffix(后缀)的,因此似乎没有办法使用。
flag{md5_7cfa0da2c09776ae}
SHA256 350
SHA256 也就是 256 个比特位。256 个比特位要撞上 199 个。如果用上一题的代码,够到 180 位都够呛。而且 SHA256 也没有公开的快速碰撞算法,似乎前面两题的方法都不可行。
仔细观察题目,注意到 SHA256 所给的 suffix 只有 1 个字符,由于可以任意请求新的 suffix,相当于这里的 suffix 可以自己任选(范围为 [a-zA-Z0-9]),而且也不再受 1 分钟的时间限制(过期了再请求一个就是)。
这似乎也是对参赛者的提示,只要在浩瀚的互联网上找到一组最后一个字节相同的、范围在 [a-zA-Z0-9] 的 nonce,并且 sha256(nonce1) 与 sha256(nonce2) 有 ≥ 199 比特位相同即可(这里的 suffix 就是 nonce1 与 nonce2 的最后一位)。
所以.. 这浩瀚的互联网,要到哪里去找?考虑到本题与区块链的紧密联系,联想到了 Bitcoin 使用的工作量证明方法(Proof of work),见:块散列算法(Block hashing algorithm),俗称挖矿。这种方法同样用到了 SHA256。
简单地说,就是不断计算 SHA256(SHA256(上一区块 Hash 值等信息)),当结果末尾的 0 比特位的个数达到难度(Difficulty)的要求,新的区块就产生了。
由于 Bitcoin 的工作量证明方法要求每个区块 Hash 值都包含大量的 0,因此这部分自然就是相同的。不妨随意拿两个区块 Hash 来看看:
# https://www.blockchain.com/btc/block-height/544535 000000000000000000096d4052ed11b1db52675ea486feb047b708493c97c709 # https://www.blockchain.com/btc/block-height/544534 0000000000000000001b7949772eef25c640852e3def79420861dcc3ba660969 # 注意实际的 Hash 经过了按字节的反转,即 Reverse(SHA256(SHA256(上一区块 Hash 值等信息)))
两个 Hash 计算出的 PopCount 为 171,远大于 128 的平均值。
由于对两个 nonce 的 Suffix 有要求(相同且在 [a-zA-Z0-9] 范围内),不妨将 Bitcoin 目前所有块的头部(目前有 50 多万个块)下载下来,按照一次 SHA256 后的最后一字节进行分类,并在每个类别里做第二次 SHA256,尝试碰撞。
(Python 字节处理不太熟,用了 PHP,速度比较慢)
<?php
$data = '';
if (!file_exists('blockchain_headers')) {
echo "Downloading blockchain_headers.\n";
$data = file_get_contents('https://headers.electrum.org/blockchain_headers');
file_put_contents('blockchain_headers', $data);
echo "Download completed.\n";
} else {
$data = file_get_contents('blockchain_headers');
}
$hashs = [];
$len = strlen($data);
$pointer = 0;
while ($pointer < $len) {
$head = substr($data, $pointer, 80);
$pointer += 80;
$hash1 = hash('sha256', $head, true);
$tail = substr($hash1, -1, 1);
if ($tail >= 'a' && $tail <= 'z' || $tail >= 'A' && $tail <= 'Z' || $tail >= '0' && $tail <= '9') {
if (!isset($hashs[$tail])) $hashs[$tail] = [];
$hash2 = hash('sha256', $hash1, true);
$hashs[$tail] []= [ 'data' => $hash1, 'sha256' => $hash2 ];
}
}
echo "Hashs generate finished.\n";
foreach ($hashs as $alphabet => $hash) {
$hash = array_reverse($hash);
$num = count($hash);
echo 'Finding in '.$alphabet.', Hashs count:'.$num."\n";
for ($i = 0; $i < $num; $i++) {
for ($j = $i + 1; $j < $num; $j++) {
$score = score($hash[$i]['sha256'], $hash[$j]['sha256']);
if ($score > 192) {
echo $score." ".bin2hex($hash[$i]['data'])." ".bin2hex($hash[$j]['data'])."\n";
}
if ($score >= 199) {
echo 'Success ^_^';
exit();
}
}
}
}
function score($hash1, $hash2) {
$c = 0;
for ($i = 0; $i < strlen($hash1); $i++) {
$k = getBitCount(ord($hash1[$i]) ^ ord($hash2[$i]));
$c += 8 - $k;
}
return $c;
}
function getBitCount($value) {
$count = 0;
while ($value) {
$count += ($value & 1);
$value = $value >> 1;
}
return $count;
}
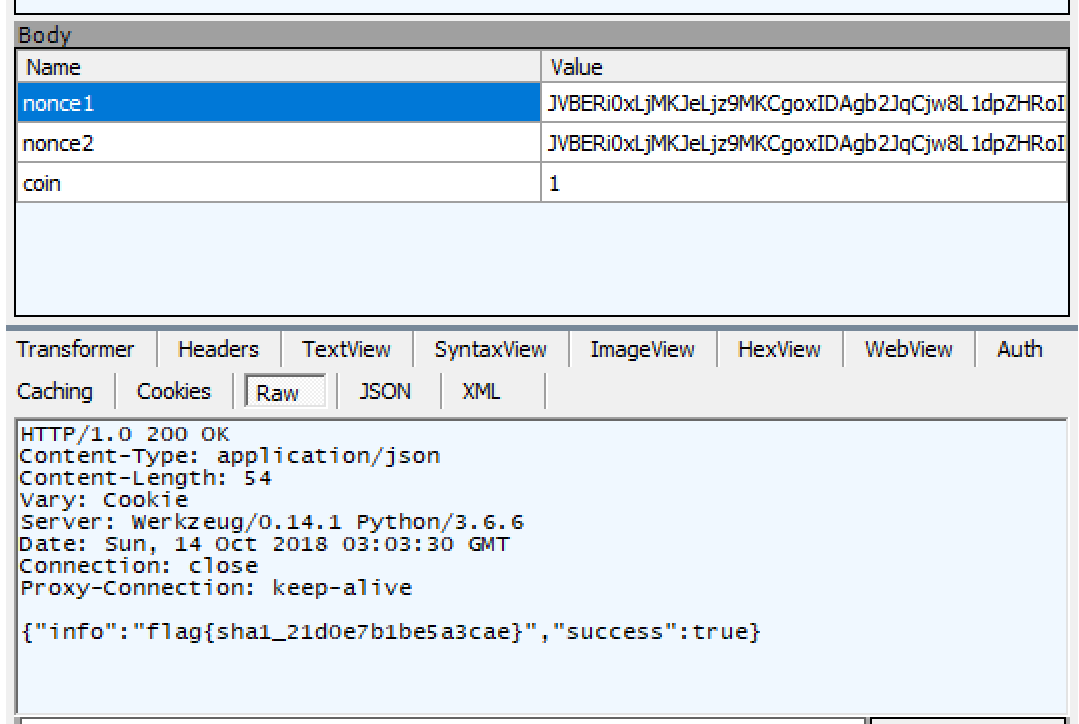
运行后正好找到一组 PopCount 为 199 的 nonce(因此我觉得这是出题者的预期解法)。由于 nonce 末尾是 0x44(D),多次请求,得到为 D 的 Suffix 后,提交 nonce 对即可获得 Flag。
flag{sha256_02938baf7abc9cd3}
加密算法和解密算法 250
主办方很贴心的给了整整一个网页的说明..
GitHub 上随便找了一个 BrainFuck 的反编译器,将代码理解并整理后,获得下面一份代码。
function encrypt(input) {
if (/^[\w-]{40}$/.test(input)) {
let index = -1, output = ''
let map = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789-_'
let write = i => output += map[i % 64], read = () => map.indexOf(input[++index])
start(write, read)
start(write, read)
start(write, read)
start(write, read)
// new BF(write, read).run(bf).run(bf).run(bf).run(bf)
return output
}
throw new Error('Invalid input format!')
}
function process(tape, ptr, arr) {
var round = tape[ptr]
tape[ptr] = 0
for (var i = 0; i < arr.length; i++) {
tape[ptr + 2 + i] += arr[i] * round
}
}
function process2(tape, ptr, arr) {
for (var i = 0; i < arr.length; i++) {
tape[ptr + i] += arr[i]
}
}
function start(write, read)
{
var size = 1000;
var tape = [];
var i = 0;
/* Clearing the tape (array) */
for (i=0; i < size; i++)
tape.push(0);
var ptr = 0;
tape[ptr] = read();
process(tape, ptr, [23, 46, 21, 80, 35, 81, 34, 19, 76, 38])
tape[ptr] = read();
process(tape, ptr, [69, 67, 80, 27, 22, 64, 79, 38, 55, 78])
tape[ptr] = read();
process(tape, ptr, [40, 40, 63, 69, 66, 51, 74, 52, 41, 43])
tape[ptr] = read();
process(tape, ptr, [61, 54, 33, 53, 43, 46, 52, 72, 68, 59])
tape[ptr] = read();
process(tape, ptr, [47, 31, 60, 37, 68, 37, 27, 49, 39, 55])
tape[ptr] = read();
process(tape, ptr, [21, 23, 26, 81, 36, 44, 19, 71, 62, 74])
tape[ptr] = read();
process(tape, ptr, [62, 54, 39, 24, 67, 75, 38, 36, 48, 50])
tape[ptr] = read();
process(tape, ptr, [73, 75, 32, 61, 22, 77, 79, 40, 65, 18])
tape[ptr] = read();
process(tape, ptr, [18, 64, 48, 23, 58, 71, 30, 60, 21, 36])
tape[ptr] = read();
process(tape, ptr, [81, 69, 39, 50, 37, 18, 68, 45, 66, 77])
ptr += 2;
process2(tape, ptr, [2, 6, 8, 8, 3, 5, 5, 7, 4, 9])
write(tape[ptr]);
ptr += 1;
write(tape[ptr]);
ptr += 1;
write(tape[ptr]);
ptr += 1;
write(tape[ptr]);
ptr += 1;
write(tape[ptr]);
ptr += 1;
write(tape[ptr]);
ptr += 1;
write(tape[ptr]);
ptr += 1;
write(tape[ptr]);
ptr += 1;
write(tape[ptr]);
ptr += 1;
write(tape[ptr]);
}
encrypt('QUICK_BROWN_FOXES_JUMP_OVER_THE_LAZY_DOG')
要解出原文,看上去只是解 10 个简单的十元一次方程,但可别忘了方程包含了 Mod 64。
用 z3 怎么也解不出(大概是方法不对),不过后来又在 GitHub 上找到了这份东西(模线性方程组在密码分析中的应用)。
使用他提供的 Python 程序求解后,最终获得 Flag。
CWK的试炼 650
神庙设计图, Get! 250
拿到一张 webp 图片。注意到原题中提到了“能避开如今的 FLXG 雷达的探测”,难道说珍藏了 3 年的 Stegsolve.jar 小工具失效了?
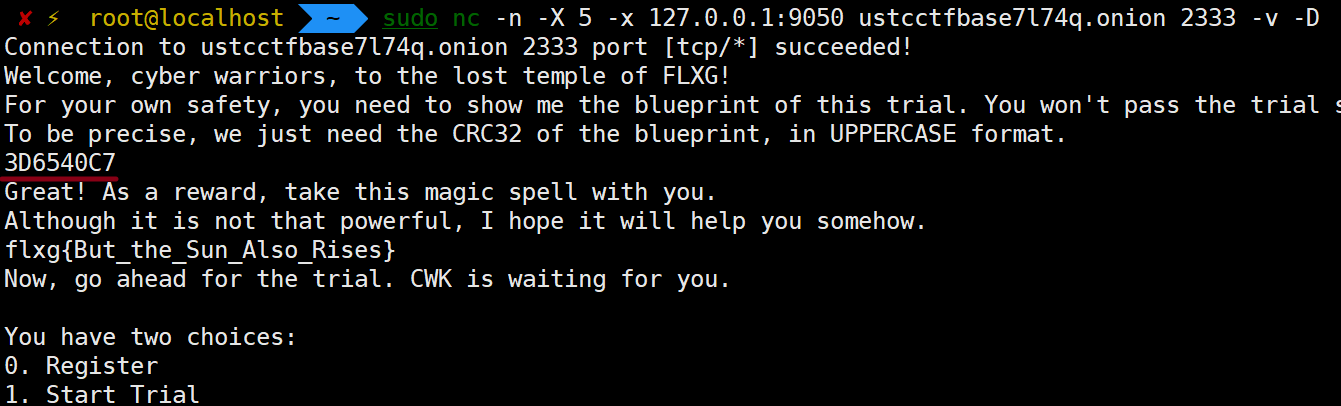
不管,先将 webp 图片转成了 png,依然丢进了 Stegsolve.jar 跑了跑,很快在绿色 LSB(最低比特位)发现了一个洋葱地址(ustcctfbase7l74q.onion)。
用一个“比较冷门的一个西方魔法”连上后发现需要提交“被 CWK 用法力嵌入到了指向神庙的地图里”的“神庙的设计图”。
地图应该指的就是那张 webp 的图片。但担心出题者将信息藏到了 webp 的文件格式中的某处,那就要学习 webp 格式再来解题了。
揣测一下出题方式。由于各大图片编辑软件还未很好的支持 webp,出题者应该是先把 png 等无损格式的图片做好,使用谷歌官方的工具(因为现在转换工具不多)转成启用了无损模式的 webp,然后再将信息藏到了 webp 的文件格式中。
不妨再将刚才转化好的 png 再转回 webp,和原图对比一下吧。
cwebp trial.png -o trial_2.webp -lossless
几次尝试后,注意到以上命令转换回的 webp 与原题文件大小一致(即无损压缩率一致),且两个文件二进制内容也一致。这时可以断定,出题者并没有将信息藏在 webp 的文件格式中。那安心分析图片内容就好了。
于是再次打开珍藏了 3 年 + 1 小时的 Stegsolve.jar 小工具,多次切换后,发现图中的岛屿有一个魔法的黑框,且切换到绿色 LSB 时,黑框中呈现了西方的纹理。
说明很可能在这里藏了数据。但是我们不能只从绿色 LSB 来提取数据,注意红框中圈出且放大的部分,有些黑色字节和黑色边框产生了粘连。我们需要结合其他颜色的数值,来判断这里的黑色是数据还是黑色边框本身。
我们将原图简单处理一下,把黑框外的部分全部改为黑色。
然后写个程序提取出黑框中的数据。
var getPixels = require("get-pixels")
const fs = require('fs')
getPixels("trial_2.png", function(err, pixels) {
if (err) {
console.log("Bad image path")
return
}
console.log("got pixels", pixels.shape.slice())
var binary = ''
var flatArray = []
var chain = 0
var total = 0
for (var y = 0; y < 699; y++) {
for (var x = 0; x < 731; x++) {
if (pixels.get(x, y, 0) == 0 && pixels.get(x, y, 1) == 0 && pixels.get(x, y, 2) == 0) { // 如果该像素为纯黑色(#000000),跳过
if (chain > 0) console.log(chain) // 输出每行的数据长度,用于检查数据是否被中间的纯黑像素点断开了(最后发现没有被断开过)
chain = 0
continue
}
chain++
total++
binary += (pixels.get(x, y, 1) & 1) ? '1' : '0'
}
}
console.log(total, total / 8) // 恰能整除,Great!
fs.writeFileSync('out', binary)
})
最终发现提取出的数据是一个 ELF 文件。原来这就是所谓的“神庙的设计图”。
将此文件 CRC32,提交到刚才的服务器,获得 Flxg。
flxg{But_the_Sun_Also_Rises}
下一小题 此小技耳 400 虽然做了很久,但最后并没有做出。一开始觉得是 Crypto + Reverse 类型的,但看了很久之后感觉是 Pwnable,于是放弃。
虽然不是非常标准的 CTF(Web 和 Pwnable 很少,Misc 比较多),但却是很有趣的 CTF。在思考与解题的过程中,也学到了不少新东西。最终排名 #3。
Coxxs










66666
6666666
tql 总想着溢出钱完全忘了时间也可控orz
tql tql
tql
太强了
很有意思,真心佩服~
orz
叉叉好厉害!!
妙妙妙
开 6149 太强了